[Swift] 프로그래머스 N-Queen - DFS

https://school.programmers.co.kr/learn/courses/30/lessons/12952

프로그래머스

 

---

조건

• 가로, 세로 길이가 n인 정사각형으로된 체스판
• 체스판 위의 n개의 퀸(Queen)이 서로를 공격할 수 없도록 배치
  • 퀸(Queen)은 가로, 세로, 대각선으로 이동

 

풀이

import Foundation

func solution(_ n:Int) -> Int {
    var ret = 0
    // maps를 통해 갈 수 있는 곳을 확인
    var maps = Array(repeating: Array(repeating: true, count: n), count: n)
    
    func dfs(_ position: [Int]) {
        let row = position.count
        
        // dfs의 중요한 종료 조건!!
        guard row < n else { ret += 1; return }
        
        var position = position
        let tmp = maps
        
        // 세로 및 대각선의 겹치는 부분을 확인하여 maps에 기록
        for (i, value) in maps[row].enumerated() where value {
            // 가로에 놓이는 것마다 놓을 수 있는 위치가 다르기에 초기화
            maps = tmp
            for j in row+1..<n {
                if 0..<n ~= i+j-row { maps[j][i+j-row] = false }
                if 0..<n ~= i-j+row { maps[j][i-j+row] = false }
                maps[j][i] = false
            }
            
            // 자세한 건 그림으로 표현
            position.append(i)
            dfs(position)
            position.removeLast()
        }
    }
    
    dfs([])
    
    return ret
}

 

그림을 통한 예시

놓여지는 게 없는 상황

반복문을 돌 수 없는 상황으로 DFS가 더이상 진행되지 않고 넘어간다.

놓여지는 게 없는 상황

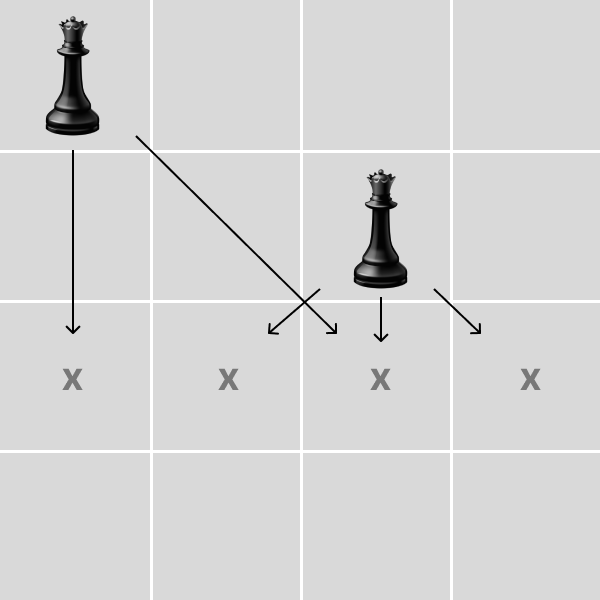
다음으로 넘어간 상황

DFS는 깊이 우선 순위로 순차적으로 진행하게 된다.

다음으로 넘어갔지만

막혔으므로 0번째 퀸은 우측으로 한 칸 이동하게 되고, 다시 깊이 우선 순위로 반복

 

---

테스트 결과

 

---

여기까지가 내가 푼 결과이고 이제 다 풀어봤으니 다른 사람의 풀이를 보면서 해석

일단 코드를 읽기는 보다 쉽다.

• 0번째 row는 반복문으로 backtrack 을 실행
• 0부터 n 미만의 숫자를 집어넣으면서 backtrack 을 재귀
• 이전 row에 놓인 값과 동일한지 현재 값과 row 값을 비교 하여 기울기와 동일한지 판단 
  • 퀸의 이동은 1, -1 기울기로 움직이기 때문에 abs로 절대값으로 확인

import Foundation

func solution(_ n:Int) -> Int {
    var queen: [Int] = Array(0..<n)
    var count: Int = 0

    func backtrack(x: Int, n: Int) {
        for i in 0..<x {
            if (queen[i] == queen[x] || abs(queen[i] - queen[x]) == abs(i-x)) {
                return
            }
        }

        if x == n - 1 {
            count += 1
            return
        }

        for i in 0..<n {
            queen[x + 1] = i
            backtrack(x: x + 1, n: n)
        }
    }

    for i in 0..<n {
        queen[0] = i
        backtrack(x: 0, n: n)
    }

    return count
}

 

속도도 빠를 줄 알았지만, 코드가 단순해졌지만 반복문이 더 많아졌기 때문에 속도는 느리다